Steering a bicycle
.
Many five-year-old kids can give a demonstration of riding a bicycle. By steering a bicycle, I mean the design and consequences of the choices of wheel diameter, fork offset and frame geometry. Which forces play a role, and which theory predicts the steering characteristics.
The low mass of the bicycle in relation to the rider, has a strong influence on the steering behavior. This is a complicating factor that is difficult to put into formulas. Around 1886, the frontfork of the Rover Safety of Fig.1a takes this shape, that is used in almost all designs.
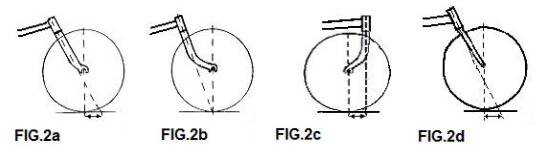
When the trail is zero (FIG.2b), the bicycle no longer has its own stability. With even more offset we get “negative trail” and the bike wants to go in all directions except straight ahead; this is tiring and dangerous! Some forks are not curved but straight. N.B. These fork sheaths do make an angle with the steerer tube, so the trail does not become too large! (See FIG. 2d). We can also can get a trail by turning the fork around, as in FIG.2c; this is used, with stayer bikes behind the derny (FIG.2e) and front-wheel-drive recumbent bikes such as Bokhorst and Minq. But they too already had a stream-lined predecessor, as evidenced by this patent application by Augustin Isaac from Lyon in 1941.
Lifting the frame while turning the handlebars, see FIG.1b, is an important effect of the fork offset V. If we turn the handlebars 90 degrees, the frame is lifted over height H. If we turn less, the frame is also lifted less. Straight ahead goes through the lowest point and that takes the least force. If more weight presses on the front wheel, such as with a tandem, more weight will have to be lifted and you will notice this effect better.
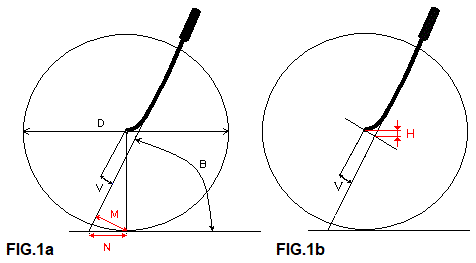
FIG.1a The geometry of the front frame. Many experiments are known with head angles (B), wheel diameters (D) and fork offset (V). We can get an offset by bending the fork (2a,2b), by angling straight fork legs with the head tube (2d), or by simply placing the fork legs a few inches in front of the steerertube. The trail N and the effective trail M (= mechanical trail, the important value) are fixed, once we have selected the first three. With B, D and V, and using some mathematical magic, we can calculate that: M = (0.5. D. Cos B - V) and N = (0.5. D. Cos B - V): sin B.

To see the effect, the researcher David Jones built bikes with fork geometries that went against all existing wisdom. He tried to build an unridable bicycle. All his creations turned out to be rideable after some practice; apparently people can adapt well: the salvation for many a designer! David Jones introduced a stability index U. Bicycles have good handling properties if they are between -1 and -3; at the higher values, like -1, the bicycle becomes more unstable; at lower values, such as -3, the self-correcting effect is greater. So you have to turn the handlebars a little further before turning, and the handlebars straighten itself faster. In the FIETS magazine, this u-value was often included in the frame data. Although the u-value is used to compare the stability of bicycles with the same wheel diameter, (as in a test of different racing bicycles), Jones's theoretical model turns out not to be good enough to give an absolute judgment.
When we keep balance on the bike, we are constantly making small corrections; we wind slightly around our own trail. Our equilibrium is determined by the position of the center of gravity (COM = center of mass) in relation to the plane through the main frame. As soon as we want to make a left turn, we first (unconsciously) steer to the right, to get the center of gravity to the left of the frame plane. Gravity now pulls us to the left and down; however, the driving speed creates a centrifugal (= "centrifugal") force that pushes us out and up again. The effect is, that we start leaning in the corner. This requires a reaction force (= grip) of the tires; we soon fall, riding on ice.
At very low speeds, the centrifugal force is lacking and we balance with our center of gravity above the contact points of the wheels. Keeping our equilibrium is harder.
Each bicycleframe, has a certain speed above wich it rides stable.The old-fashioned granny bike is more stable than a criterium racer. Usually these values are around 20 km / h (6 m / s). At this speed, the bike will be stable even without a rider and correct minor disturbances itself! In experiments with a riderless bicycle, use was made of small flares that were mounted on the handlebars. If the bicycle did not stabilize itself, and after ignition the handlebars turned to the left, the bicycle fell over to the right! This proves that we are steering left to go right. If the speed of the riderless bicycle becomes too low or too high, the bicycle will slowly tip over in a slow left or right turn.
The rider's arms act as a damper to vibrations. This is an important function: without damping, vibrations can grow into a shimmy; this is an increasing vibration around the longitudinal axis of the vehicle. Shimmies have to do with the natural frequency of the vehicle and occur at a specific speed for that bicycle. A cause of the occurrence of vibrations is the pedaling frequency. The place where we apply force, the pedal, is outside the plane through the frame and wheels. Certainly if we pedal firmly, there will be a shift in the balance, which can cause a slight sway in the handlebars. Since there are two pulses per revolution of the cranks, the frequencies are usually between 1.5 and 4 Hertz. The eigenvalues of the frame should be above 5 Hertz. Regular vibrations of the road surface (cobblestones or ridges) can also cause annoying frequencies and swinging effects.
The height of a bicycle's center of gravity influences our steering corrections. The higher, the more time we have to correct. As long as we drive straight ahead, a low center of gravity is more stable. This advantage disappears if we have to react quickly to avoid pits or stones. The weight distribution (location and height of the center of gravity) is important; with a lot of weight on the front wheel, the bicycle will react more quickly to turning the handlebars. The wheelbase also has a major influence on the handling of the bicycle. Long bicycles, like tandems, are much more stable than their one-person colleague with the same geometry. They obviously need more road surface to maneuver. Folding bikes and short wheelbase recumbents and are notoriously nervous, but extremely nimble. There are recumbent bicycles where the rider can turn a circle with one hand on the ground. On a granny bike almost all the weight rests on the rear wheel; this is a case of "understeer": the steering angle is relatively large before the turn is initiated. If you transport all the camping gear on the rear carrier on a holiday, you get the same effect. If you go to the bakery for a moment, once you have set up the tent, you have to get used to direct steering of the bicycle again. If you mount a time-trial handlebar, there is more weight on the front wheel and the bike tends to "oversteer". Even at a small steering angle, you already are going into the corner.
We call everything that rotates with the handlebars, the front frame. It is nice if the center of gravity of the front frame is as close as possible to the rotation axis of the steering tube. Child seats and luggage carriers attached to the front frame are a pain. There are several forces that act on the front frame of the bicycle. The most important is the steering torque, the force that the rider exerts on the handlebars. The kinetic energy, the gyroscope effect in our front wheel, provides extra stability. This is the well-known trick of laboriously turning a rotating wheel in your hands; this force is small compared to the steering torque, but increases with the peripheral speed and the mass of the wheel. Another stabilizer is the geometric force, which is produced by the trail. This increases as the effective trail M (mechanical trail) from FIG.1 increases. These three forces work together to keep the bike running straight. There are even more forces acting on the front frame, such as the friction of the tires and aerodynamic forces (especially with a closed front wheel). The impact forces from bumps and potholes in the road surface also reach us, through the front frame. In experiments, the gyroscope force was eliminated by means of a counter-rotating flywheel. The bicycle will then become less stable (almost impossible to ride with free hands), but it remains steerable. Good bicycle designs are self correcting; the bicycle will want to go straight again after hitting a bump. When the handlebars rotate, the bicycle will follow an initiated curve determined by the geometry,. A criterium racer must be able to change direction very quickly; the builder then opts for little stability.
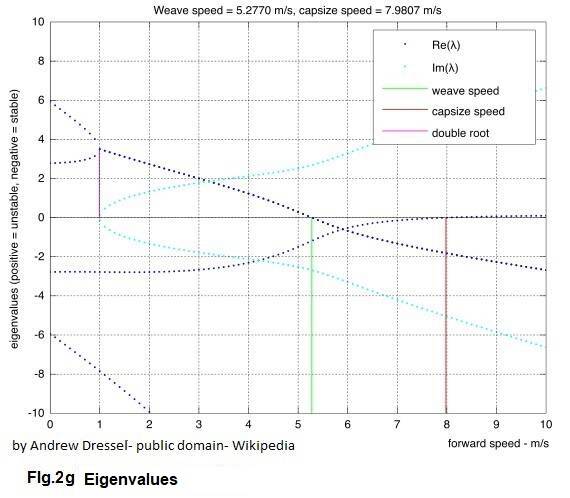
The bicycle frame only rides stable within a certain speed range; this stable region has an upper limit (see FIG.2g). If the speed of a riderless bicycle becomes too low, the bicycle will wobble and fall over; at speeds above the stable area, the riderless bicycle will fall over in a slow bend to the left or right (capsize). To be stable, the eigenvalues must be negative (the blue dot-lines, graph 2g); at low speed (runout) the eigenvalues are negative from 5.3 m / s; from this speed the bicycle is stable until the capsize speed is reached at 8.0 m / s.
Bill Patterson has put a lot of effort into finding a formula to choose good geometry for a wide variety of bikes. The core of his argument is that at low speed, the bicycle wants to make a turn on its own (positive spring force) and resists turning of the handlebars at higher speed (negative spring force). In his articles he has described in detail how the measurements of the important data should take place. Nowadays the formula can also be applied via the internet.
Some recumbent bicycles differ greatly in geometry. The Flevobike has a long trail and is steered from the hips. That takes some getting used to and is easier to learn on the three-wheeled version. The Python even has a negative trail and the only stabilizing factor is now the lifting of the frame when turning the handlebars. Rear wheel steered two-wheelers are very skittish. Dennis Renner's, FIG.3c, has a limited rotation due to twisting of the seat and appears to be sufficiently stable.

Tricycles with two steering front wheels have a similar steering problem to the car. When we make a turn with such a tricycle, the wheel on the inside will have to make a smaller turning circle than the outer wheel. Both wheels are by means of the steering linkage. The shape of the trapezoid is determined by the distance to the center of the rear axle: the Ackerman principle (FIG.4a). Energy losses can occur in the control system due to poor tracking (not running parallel of the wheels). When the wheels point inward, there is “toe-in”; "Toe-out" means the wheels pointing outwards, this leads to unstable behavior and must be avoided! Both provide additional friction and tire wear
If the angle between front wheel and road surface is chosen such that the center line through the steering axle intersects the road surface on the plane through the wheel, this is called center point control (see FIG.4c) the center line through the steering axels cuts the road surface through the plane of the wheel . Usually this is applied to 3 or 4 wheelers, but sometimes on modern two-wheelers. The steering axle in this case, is mounted in the middle of the wheel. The wheel will have the shape of a pan lid. Certainly if you take a single steering front wheel with steering axle, you should opt for center point steering. With construction according to FIG.4c, you may not mount wider or narrower tires and you cannot install suspension, because then the bike will no longer track. The pivot point of the wheels is formed by the steering axles (Kingpin) F (see FIG.4b). These should slope inwards (5-10 °) and backwards. A disadvantage of centerpoint steering is that play in the assembly or the king pin can quickly lead to a so-called. shimmy ! This is a vibration around the longitudinal axis of the vehicle. Using two steering front wheels, we chose a somewhat steeper angle ( King Pin Inclination or K.P.I.); the point of intersection with the road surface is now between the wheels. The distance between the intersection point and the wheel is called the scrub radius. Both values determine the steering behavior of the tricycle, especially stability and the self-correcting effect when exiting the corner. A larger scrub radius results in a better self-correcting behavior. But the steering becomes sluggish and it takes energy. This is due to extra friction (and therefore extra wear on the tires). Centerpoint steering is often used for Human Powered Vehicles, but in particular to improve stability at top speed, deliberate deviations from the Ackerman principle and / or light toe-in are chosen.

.
In FIG.5 we see a tricycle with rear wheel steering from 1985 from the Dutch manufacturer Jouta. The handling of this tricycle, is not self-stabilizing. Using front-wheel steering, the vehicle will want to go straight on by itself after exiting the bend, like a car; with a rearwheel steered bike, you have to keep steering. The front part of the bicycle leans in the corner; just like a two-wheeler. Only that angle of inclination is not determined by the speed, but by the head angle of the rear. A compromise arises: when taking the corner too slow, the rider wants to fall inward. When taking the corner too fast, the rider wants to go outside. The construction is simple and due to the low center of gravity, the road handling is reasonably stable. The wheels of a tricycle experience lateral forces when cornering; so choose thicker spokes and / or smaller wheels. Keep in mind that the brakes on the parallel wheels apply with the same force: otherwise it will want to turn a corner! The choice for a single steering rear wheel is also possible, which can be found at the American Sidewinder. At higher speeds (> 40 km / h) these tricycles are not really stable; a steering damper can help prevent shimmies.
In-depth calculations have resulted in new insights into bicycle stability. The combination of people from Dutch Delft university of technology (Schwab, Kooiman, Meijaard) and Cornell University (Ruina, Papadopoulos, Hand) has paid off. Based on theoretical calculations, a two-wheeler has been built with a small negative trail, while the gyroscopic forces of the wheels are canceled by counter-rotation. Thinking traditionally, such a combination could never produce a self-stabilizing bicycle; nevertheless, the bicycle is stable, which proves the correctness of the theoretical model. This bike is not yet a new frame design, but just a refined riderless scooter with roller skate wheels. We are curious whether real bicycles can also be made based on this calculation model.
TEN SLOTTE: LEESVOER EN DOWNLOADS VIA HET WWW:
Een rekenprogramma naar aanleiding van de artikelen van Bill Patterson vindt u op: http://www.wisil.recumbents.com/wisil/trail.asp
Sheldon Brown via de pagina's van Jobst Brandt: http://www.sheldonbrown.com/brandt/gyro.html Er staat ook nog een artikel over shimmy's.
T.Foale: www.tonyfoale.com/Articles/index.htm o.a.: Basic principles of Balancing en Experiments with steering geometrie (engels-MBOniveau)
https://www.cyclingabout.com/understanding-bicycle-frame-geometry/
Boeken: Bicycling Science - D.G. Wilson ( with contributions of J.Papadopoulos ) third edition 2004 ISBN: 0-262-73154-1
Motorcycle Handling and Chassis Design: The Art and Science - T. Foale second edition 2006 ISBN: 8493328634
Er is een nieuwe kijk op fietsbesturing met veel inbreng van TU-Delft, in combinatie met Cornell University, maar dit is voor liefhebbers met een wiskundeknobbel, zie: http://www.bicycle.tudelft.nl/ en http://ruina.tam.cornell.edu/research/topics/bicycle_mechanics/stablebicycle/index.htm
A simpler story: https://www.youtube.com/watch?v=9cNmUNHSBac
Hier vind je de ontwikkeling van de theorie: J. Meijaard, J. Papadopoulos, A. Ruina, A. Schwab: Historical Review of Thoughts on Bicycle Selfstability
Daarnaast staat er ook een duidelijk uitgewerkt onderzoek met de pakkende titel: 1201959SOMtext.pdf
J.D.G. Kooijman: Experimental Validation of a Model for the Motion of an Uncontrolled Bicycle (T.U.niveau)
Jaap Meijaard c.s.: Linearized dynamics equations for the balance of a bicycle: a benchmark and review (T.U.niveau)
Een robot: https://www.youtube.com/watch?v=mT3vfSQePcs
Ook leuk, Human Power USA: http://www.hupi.org/HPeJ/